
執筆
ヤマハ発動機株式会社
生産技術部鍛造技術グループ
石川 健吾、牧野 則俊
論文要旨
当社の電動アシスト自転車ドライブユニットに使用される歯車部品は、ラチェットとヘリカルギアが1部品内に設けられた設計となっており、ドライブユニットのコンパクト化・軽量化に貢献している。ラチェット部の成形は、生産効率の良い鍛造工法が採用されており、鍛造品特有の延性割れ不良を防ぐため、精密冷間鍛造2工程で量産されている。
生産効率の更なる向上と、製造コスト削減のため、精密冷間鍛造工程の1工程化が求められている。また、延性割れを予測する解析技術の開発が課題となっている。
本研究では、鍛造ラチェットの延性割れメカニズムと、コストダウンに向けた技術検証を報告する
はじめに
電動アシスト自転車市場は、グローバル規模で力強い成長を続けている。世界新商品として1993年に産声を上げたヤマハPAS(Fig.1)は、2023年に誕生30年の節目を迎える。自転車の持つ手軽さや利便性に加え、動力源に化石燃料を必要としない、“人に地球にやさしいパーソナルコミューター”を開発コンセプトとして、当社では製品の機能向上や普及に取り組んでいる。
モーターアシスト力を供給するドライブユニット(Fig.2)の機能向上には、モーターの高出力化に加え、ハウジングや歯車部品等のコンパクト化・軽量化が求められる。
本研究の対象部品(Fig.3)は、人がペダルを漕ぐ力とモーターアシスト力をチェーンへ伝達する歯車部品であり、2つの動力はそれぞれ、ラチェットとヘリカルギアから伝達される。2種のギアが1部品内に設けられた設計は、ドライブユニットのコンパクト化・軽量化に貢献している。 本稿では、精密冷間鍛造技術によるラチェット成形について、延性割れ不良のメカニズムと、コストダウンに向けた技術検証を報告する。

Fig.1 電動アシスト自転車PAS Fig.2 ドライブユニット Fig.3 対象歯車部品
部品説明
2-1.ラチェット歯車の機能
ドライブユニットの構造と対象部品図をFig.4に示す。対象部品は、ドライブユニットのペダル軸に取り付けられ、ペダルを漕ぐ力はラチェットから(赤矢印)、モーターアシスト力はヘリカルギアから(青矢印)伝達される。
ラチェット形状をFig.5に示す。人がペダルを漕いだとき、ラチェット歯とラチェット爪が噛合うことで踏力が伝達され(赤矢印)、ペダルを漕がないとき空転する(青矢印)。 スムーズな駆動切り替えには、ラチェット形状が精密に成形されている必要があり、工法には高精度が求められる。部品内面に設けられたラチェットの成型は、機械加工では生産効率が低い為、精密冷間鍛造による高効率なラチェット成形を行っている。
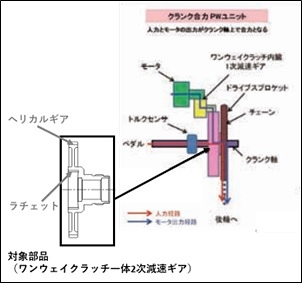
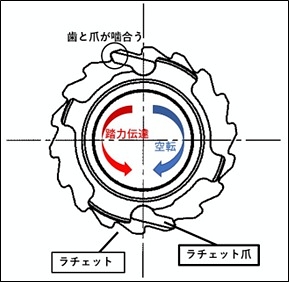
Fig.4 ドライブユニットの構造と対象部品図 Fig.5 ラチェット形状
2-2.ラチェット歯車の量産工程
Fig.6に対象部品の量産工程を示す。ラチェット形状は冷間鍛造2工程で成形される。冷間鍛造①と冷間鍛造②の間に焼鈍処理を施し、ひずみを低減させることで、歯面割れ不良の発生を防いでいる。
試作段階で、冷間鍛造1工程での成形を検証したが、全歯に歯面割れ不良が発生した。(Fig.7)歯面割れ不良の様子から、“延性割れ不良”が発生したことが確認できる。
以降、冷間鍛造1工程でのラチェット成形を“試作仕様”、冷間鍛造2工程でのラチェット成形を“量産仕様”と称す。(Fig.8)
生産効率の向上と製造コスト削減の為、量産仕様の1工程化が求められている。また、延性割れを予測する解析技術の開発が課題となっている。
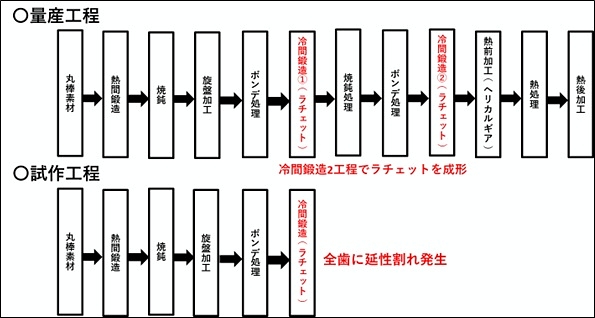
Fig.6 鍛造ラチェットの工程
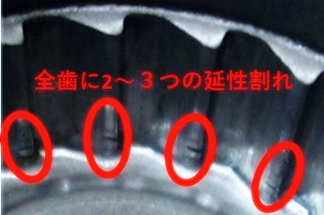
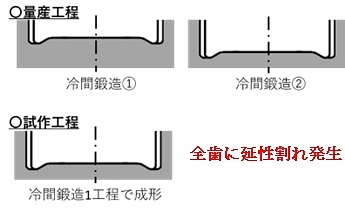
Fig.7 試作時のラチェット歯面割れ不良
Fig.8 冷間鍛造工程の模式図量産工程(上図)
試作工程(下図)
CL式による延性割れの予測
鍛造成形における不良発生を事前に検証する手段として、鍛造シミュレーション解析を用いている。対象部品においても、実機検証前に鍛造シミュレーション解析を行った。
鍛造シミュレーションの際、延性割れを予測する手法として、延性破壊条件式がある。試作仕様、量産仕様の延性割れ予測には、Cockcroft-Lathamの式(式1)として知られる延性破壊条件式を使用した。以降、Cockcroft-Lathamの式をCL式と称す。
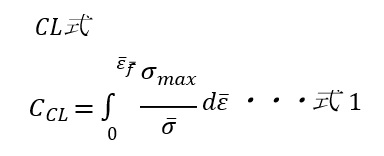
(𝐶𝐶𝐿:ダメージ値𝜎̅:相当応力、𝜎𝑚𝑎𝑥:最大主応力、𝜀̅:相当ひずみ、𝜀̅𝑓:延性割れ発生時のひずみ)
延性破壊条件式は、材料内の任意点が、成形開始~成形終了の間に、応力とひずみによって受けるダメージを計算する式である。ここで、ダメージのパラメータとされるダメージ値がある一定の値(限界ダメージ)を超えたとき延性割れが発生する。CL式は、材料内の任意点で発生する3方向の主応力のうち、最大主応力𝜎𝑚𝑎𝑥(引張応力)のみを考慮した式であり、特に単軸引張応力場でのダメージ計算に適する。
試作仕様のダメージ値をFig.9に示す。ラチェット歯面上4点に解析ポイントをプロットし(Fig.10)、各ポイントにおけるダメージを計算した。計算結果として、歯面中央のポイント3で最大ダメージ値を示した。一方、実機試作では歯面底部に近いポイント1~ポイント2の範囲で延性割れが発生した。ダメージ計算における最大ダメージ位置と、実際の延性割れ位置が一致しないことが分かる。次項では、最大ダメージ位置と延性割れ位置が一致しない要因を検討し、対策を行う。
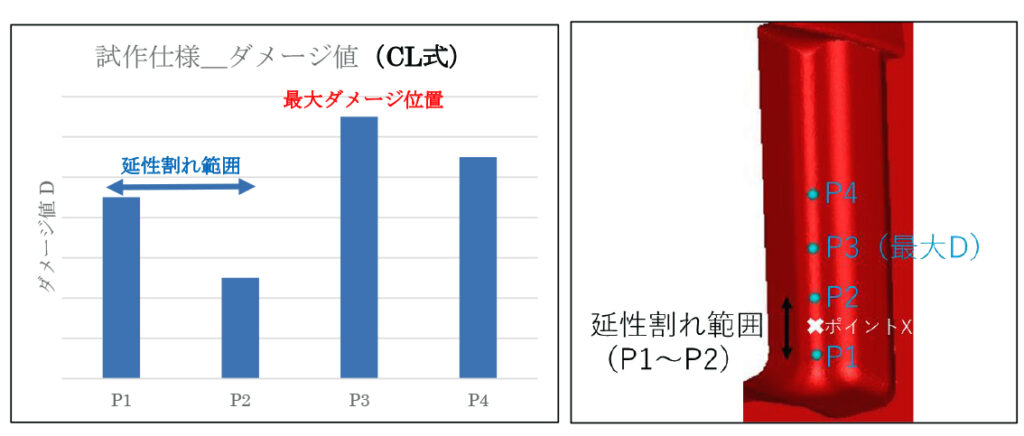
Fig.9 試作仕様_ダメージ値 Fig.10 解析ポイント4点(P1~P4)
改良式による延性割れの予測とコストダウン検証
前項で述べた通り、CL式は単軸引張応力場のダメージ計算に適する。本研究のラチェット成形に、CL式を適用できるのか、ラチェット成形中の応力場から検討する。
実機試作で延性割れが発生した範囲(ポイント1~ポイント2)の中央、ポイントX(Fig.10)の応力場を確認する。ポイントXにおける成形開始~成形終了までの最大主応力の推移グラフをFig.11に示す。成形初期は最大主応力が負で、成形途中から正に遷移していることが分かる。ここで、最大主応力が負の状態は、最大/最小/中間主応力のすべてが圧縮の応力場であり、引張応力は発生しない。最大主応力が正の状態は、最大/最小/中間主応力のうち、少なくとも1つの主応力が引張の応力場である。このことから、本研究のラチェット成形は、成形初期は圧縮応力による変形、成形途中からは引張応力による変形が進行する複雑な応力場であることが分かる。その為、ダメージ値の計算には、圧縮と引張、2種類の応力によるダメージを計算できる延性破壊条件式が望ましい。しかし、CL式では最大主応力(引張応力)によるダメージしか考慮されていない。成形初期の圧縮応力によるダメージの蓄積を考慮できていなかったことが、最大ダメージ位置と延性割れ位置が一致しない要因であると考える。
その為、圧縮応力によるダメ―ジを計算できる様、CL式を改良した。改良式を式2に示す。
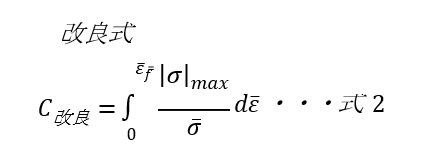
(𝐶改良:ダメージ値、𝜎̅:相当応力、|𝜎|𝑚𝑎𝑥:各主応力絶対値の最大値、𝜀̅:相当ひずみ、𝜀̅𝑓:延性割れ発生時のひずみ)
改良式内、|𝜎|𝑚𝑎𝑥(各主応力絶対値の最大値)は、最大/最小/中間主応力のうち、絶対値が最大となる主応力を取る為、圧縮場では最小主応力𝜎𝑚𝑖𝑛、引張場では最大主応力𝜎𝑚𝑎𝑥によるダメージを計算できる。
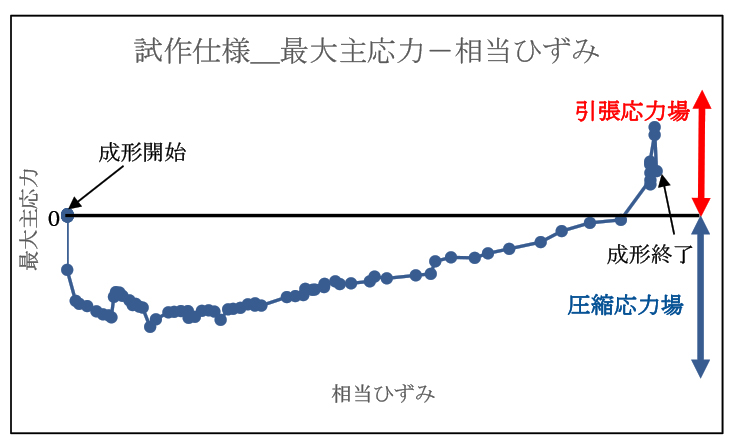
Fig.11 試作仕様_最大主応力推移グラフ
4-2.改良CL式の計算結果と妥当性の検証
Fig.12に改良式を使用したダメージ値を示す。試作仕様について、最大ダメージ値はポイント1を取り、実機試作において延性割れが発生した範囲(ポイント1~ポイント2)で高いダメージ値を示した。量産仕様冷間鍛造2工程目について、ポイント1で最大ダメージ値を示し、ダメージ値は試作仕様の半分以下の値となった。
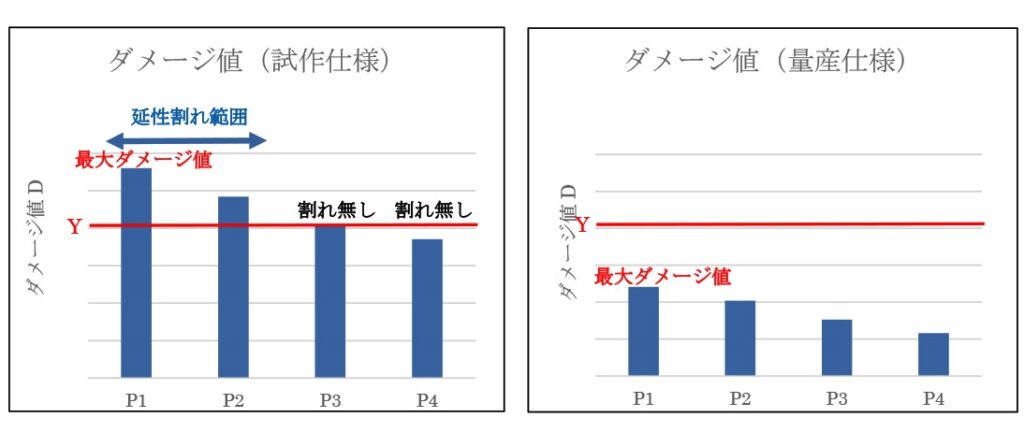
Fig.12 改良式を使用したダメージ値計算結果
改良式の妥当性を検証する為、ラチェット部表層の内部硬度を測定した。Fig.13に各測定ポイント(シミュレーションポイントに相当する4点)の硬度を示す。ダメージ値の増加に伴い、硬度も高い値となり、ダメージ値(改良式)と硬度の相関係数は0.98を示した。高い相関が見られた理由として、次のことを考察する。ダメージ値の増大は、応力𝜎とひずみ𝜀の増大によって起こる。このうち、ひずみ𝜀の増大箇所は加工硬化の影響を受け、硬度として高い値を示した。
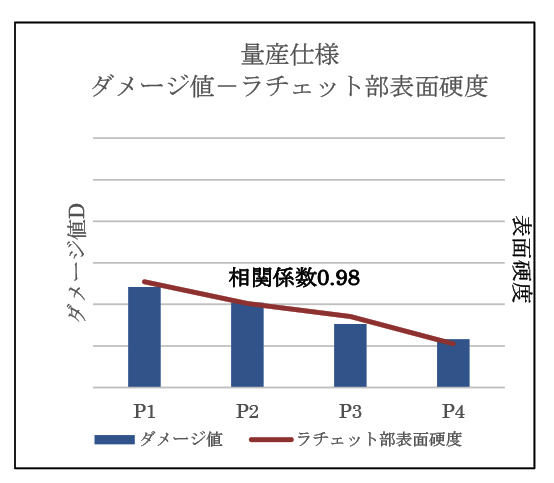
Fig.13 量産仕様におけるダメージ値(改良式)-歯面硬度の相関グラフ
4-3.改良CL式を使った対象部品の工程改善
Fig.12試作仕様ダメージ値計算結果(改良式)から、ポイント3~ポイント2の間に延性割れ発生の限界ダメージ値があると考えられる。このことから、ダメージ値をポイント3での値(ここで、ダメージ値Yとする。)以下にコントロールできれば、冷間鍛造1工程で延性割れが発生しないラチェット成形が可能になると考える。ダメージ値Y以下を狙い、材料流動を改善した新工法でのダメージ値計算結果(改良式)をFig.14に示す。
最大ダメージ値はポイント2を取り、ダメージ値Yを下回った。Fig.15に新工法で成形したワークの写真を示す。新工法による成形では、延性割れは発生しなかった。また、ラチェット部表層の内部硬度を測定した結果、量産仕様の硬度から大きく低減した。
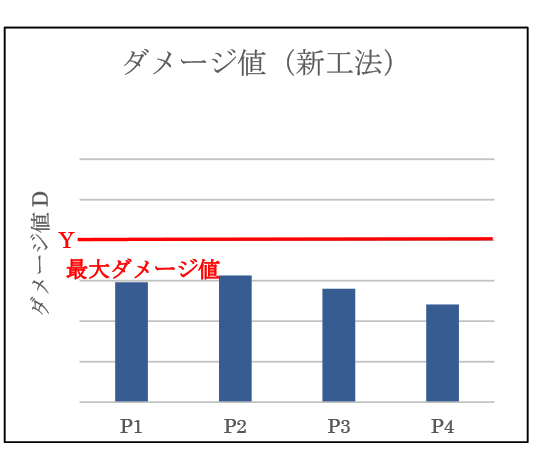

Fig.14 新工法におけるダメージ値(改良式) Fig.15 新工法で成形したワーク
まとめ
精密冷間鍛造によるラチェット成形で発生する延性割れについて、本研究から得られた結論は以下のとおりである。
(1)延性割れ発生のメカニズムについて、成形初期は圧縮応力による変形(ひずみ)、成形途中から引張応力による変形(ひずみ)が進行し延性割れに至る。
(2)本件のような成形の場合、延性破壊条件式には、圧縮応力場と引張応力場、各応力場でのダメージを計算できる式が望ましく、引張応力場でのダメージのみを計算するCL式は適さない。
(3)圧縮応力場でのダメージも計算できるよう、CL式を改良してダメージを計算した結果、最大ダメージ位置と延性割れ位置はおよそ一致した。また、ダメージ値(改良式)と歯面硬度には高い相関が見られた。
(4)最大ダメージ値(改良式)の低減を狙った新工法で実機検証を行ったところ、延性割れは発生しなかった。精密冷間鍛造工程の1工程化によるコストダウンの見込みを立てることが出来た。
参考文献
(ⅰ).岩手大学大学院松本図南著「SEM-EBSDを用いた精密鍛造部品の延性割れメカニズムの解明」
(ⅱ).塑性と加工(2019年8月号)渡邉敦夫、早川邦夫、藤川真一郎、志賀則幸著
「異方損傷モデルによる冷間鍛造における延性破壊の予測手法」
(ⅲ).軽金属第59巻第7号(2009年)、石川孝司著「塑性加工シミュレーションの現状と動向」
(ⅳ).ヤマハ発動機報第50号(2014年)、島田慎也著「PASPWユニットの開発」
新着記事
せつびさんとカンリさんの「モノづくり品質の基本のキ」#11 良い仕事をするための基本~その9 「継続的改善」
2026.02.18

ものづくり屋視点による労働衛生の実践 No.11 メンタルヘルス問題の認識と向き合う活動―その2
2026.02.18

指標でモノづくりを評価しよう! #10 納期遵守率
2026.01.28 無料会員

DXの活用がカギ! 生まれの良い設備づくり ②
2026.01.28
せつびさんとカンリさんの「モノづくり品質の基本のキ」#10 良い仕事をするための基本~その8 「事実に基づく管理 管理のサイクル」
2026.01.15

ものづくり屋視点による労働衛生の実践 No.10 メンタルヘルス問題の認識と向き合う活動―その1
2026.01.15


